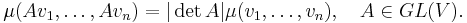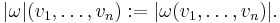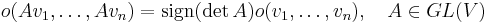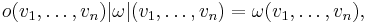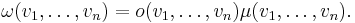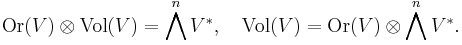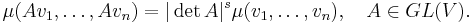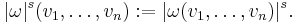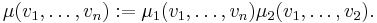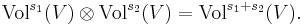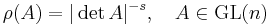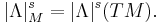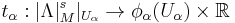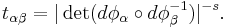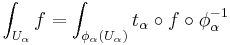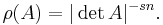Density on a manifold

In mathematics, and specifically differential geometry, a density is a spatially varying quantity on a differentiable manifold which can be integrated in an intrinsic manner. Abstractly, a density is a section of a certain trivial line bundle, called the density bundle. An element of the density bundle at x is a function that assigns a volume for the parallelotope spanned by the n given tangent vectors at x.

From the operational point of view, a density is a collection of functions on coordinate charts which become multiplied by the absolute value of the Jacobian determinant in the change of coordinates. Densities can be generalized into s-densities, whose coordinate representations become multiplied by the s-th power of the absolute value. On an oriented manifold 1-densities can be canonically identified with the n-forms on M. On non-orientable manifolds this identification cannot be made, since the density bundle is the tensor product of the orientation bundle of M and the n-th exterior product bundle of T*M (see pseudotensor.)

1 Motivation (Densities in vector spaces)
- 1.1 Orientations on a vector space
- 1.2 s-densities on a vector space
2 Definition
3 Integration
4 Conventions
5 Properties
6 References

Motivation (Densities in vector spaces)

In general, there does not exist a natural concept of a "volume" for a parallelotype generated by vectors v₁,...,v_n in a n-dimensional vector space V. However, if one wishes to define a function μ:V×...×V→R that assigns a volume for any such parallelotype, it should satisfy the following properties:

If any of the vectors v_k is multiplied by λ∈R, the volume should be multiplied by |λ|.
If any linear combination of the vectors v₁,...,v_j_-1,v_j₊₁,...,v_n is added to the vector v_j, the volume should stay invariant.

These conditions are equivalent to the statement that μ is given by a translation-invariant measure on V, and they can be rephrased as

$\mu(Av_1,\ldots,Av_n)=|\det A|\mu(v_1,\ldots,v_n), \quad A\in GL(V).$

Any such mapping μ:V×...×V→R is called a density on the vector space V. The set Vol(V) of all densities on V forms a one-dimensional vector space, and any n-form ω on V defines a density |ω| on V by

$|\omega|(v_1,\ldots,v_n)�:= |\omega(v_1,\ldots,v_n)|.$

Orientations on a vector space

The set Or(V) of all functions o:V×...×V→R that satisfy

$o(Av_1,\ldots,Av_n)=\operatorname{sign}(\det A)o(v_1,\ldots,v_n), \quad A\in GL(V)$

forms a one-dimensional vector space, and an orientation on V is one of the two elements o∈Or(V) such that |o(v₁,...,v_n)|=1 for any linearly independent v₁,...,v_n. Any non-zero n-form ω on V defines an orientation o∈Or(V) such that

$o(v_1,\ldots,v_n)|\omega|(v_1,\ldots,v_n) = \omega(v_1,\ldots,v_n),$

and vice versa, any o∈Or(V) and any density μ∈Vol(V) define an n-form ω on V by

$\omega(v_1,\ldots,v_n)= o(v_1,\ldots,v_n)\mu(v_1,\ldots,v_n).$

In terms of tensor product spaces,

$\operatorname{Or}(V)\otimes \operatorname{Vol}(V) = \bigwedge^n V^*, \quad \operatorname{Vol}(V) = \operatorname{Or}(V)\otimes \bigwedge^n V^*.$

s-densities on a vector space

The s-densities on V are functions μ:V×...×V→R such that

$\mu(Av_1,\ldots,Av_n)=|\det A|^s\mu(v_1,\ldots,v_n), \quad A\in GL(V).$

Just like densities, s-densities form a one-dimensional vector space Vol^s(V), and any n-form ω on V defines an s-density |ω|^s on V by

$|\omega|^s(v_1,\ldots,v_n)�:= |\omega(v_1,\ldots,v_n)|^s.$

The product of s₁- and s₂-densities μ₁ and μ₂ form an (s₁+s₂)-density μ by

$\mu(v_1,\ldots,v_n)�:= \mu_1(v_1,\ldots,v_n)\mu_2(v_1,\ldots,v_2).$

In terms of tensor product spaces this fact can be stated as

$\operatorname{Vol}^{s_1}(V)\otimes \operatorname{Vol}^{s_2}(V) = \operatorname{Vol}^{s_1%2Bs_2}(V).$

Definition

Formally, the s-density bundle Vol^s(M) of a differentiable manifold M is obtained by an associated bundle construction, intertwining the one-dimensional group representation

$\rho(A) = |\det A|^{-s},\quad A\in \operatorname{GL}(n)$

of the general linear group with the frame bundle of M. More precisely,

The resulting line bundle is known as the bundle of s-densities, and is denoted by

$|\Lambda|^s_M = |\Lambda|^s(TM).$

A 1-density is also referred to simply as a density.

More generally, the associated bundle construction also allows densities to be constructed from any vector bundle E on M.

In detail, if (U_α,φ_α) is an atlas of coordinate charts on M, then there is associated a local trivialization of 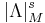$|\Lambda|^s_M$

$t_\alpha�: |\Lambda|^s_M|_{U_\alpha} \to \phi_\alpha(U_\alpha)\times\mathbb{R}$

subordinate to the open cover U_α such that the associated GL(1)-cocycle satisfies

$t_{\alpha\beta} = |\det (d\phi_\alpha\circ d\phi_\beta^{-1})|^{-s}.$

Integration

Densities play a significant role in the theory of integration on manifolds. Indeed, the definition of a density is motivated by how a measure dx changes under a change of coordinates (Folland 1999, Section 11.4, pp. 361-362).

Given a 1-density ƒ supported in a coordinate chart U_α, the integral is defined by

$\int_{U_\alpha} f = \int_{\phi_\alpha(U_\alpha)} t_\alpha\circ f\circ\phi_\alpha^{-1}$

where the latter integral is with respect to the Lebesgue measure on Rⁿ. The transformation law for 1-densities together with the Jacobian change of variables ensures compatibility on the overlaps of different coordinate charts, and so the integral of a general compactly supported 1-density can be defined by a partition of unity argument. Thus 1-densities are a generalization of the notion of a volume form that does not necessarily require the manifold to be oriented or even orientable. One can more generally develop a general theory of Radon measures as distributional sections of 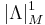$|\Lambda|^1_M$ using the Riesz representation theorem.

The set of 1/p-densities such that 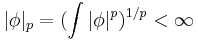$|\phi|_p = (\int|\phi|^p)^{1/p} < \infty$ is a normed linear space whose completion 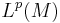$L^p(M)$ is called the intrinsic L^p space of M.

Conventions

In some areas, particularly conformal geometry, a different weighting convention is used: the bundle of s-densities is instead associated with the character

$\rho(A) = |\det A|^{-sn}.$

With this convention, for instance, one integrates n-densities (rather than 1-densities). Also in these conventions, a conformal metric is identified with a tensor density of weight 2.

Properties

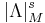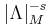The dual vector bundle of $|\Lambda|^s_M$ is $|\Lambda|^{-s}_M$ .
Tensor densities are sections of the tensor product of a density bundle with a tensor bundle.

References

Berline, Nicole; Getzler, Ezra; Vergne, Michèle (2004), Heat Kernels and Dirac Operators, Berlin, New York: Springer-Verlag, ISBN 978-3-540-20062-8 .
Folland, Gerald B. (1999), Real Analysis: Modern Techniques and Their Applications (Second ed.), ISBN 978-0-47131716-6, provides a brief discussion of densities in the last section.
Nicolaescu, Liviu I. (1996), Lectures on the geometry of manifolds, River Edge, NJ: World Scientific Publishing Co. Inc., ISBN 9789810228361, MR 1435504